What is a quantum computer?

Quantum computers are poised as an emerging technology, capturing the attention and investment of companies like IBM and Google. By name alone, few would fault the assumption that quantum computers are just faster computers. However, quantum computers require us to fundamentally rethink how algorithms can work.

Quantum computers were hypothesized by Richard Feynman and Yuri Manin in the 1980s as potential means of quantum simulation, an attempt at simulating small objects like the water molecule to get a better idea of its chemical properties. Unfortunately, for most applications, such simulations for material and drug discovery have been found to be impractical, even for supercomputers. Quantum computers also have applications in encryption, financial modeling, machine learning, differential equations, and linear algebra. Unlike a normal computer, quantum computers typically require extremely expensive and sensitive equipment. For example, IBM’s quantum computer requires IBM Goldeneye, the world’s largest dilution refrigerator, just to keep operational due to the highly sensitive nature of quantum computers. A quantum computer can still perform all computations a classical computer can in theory, meaning it is strictly computationally superior to classical computers. Quantum computers rely on three unique phenomena for such an advantage: superposition, entanglement, and interference.

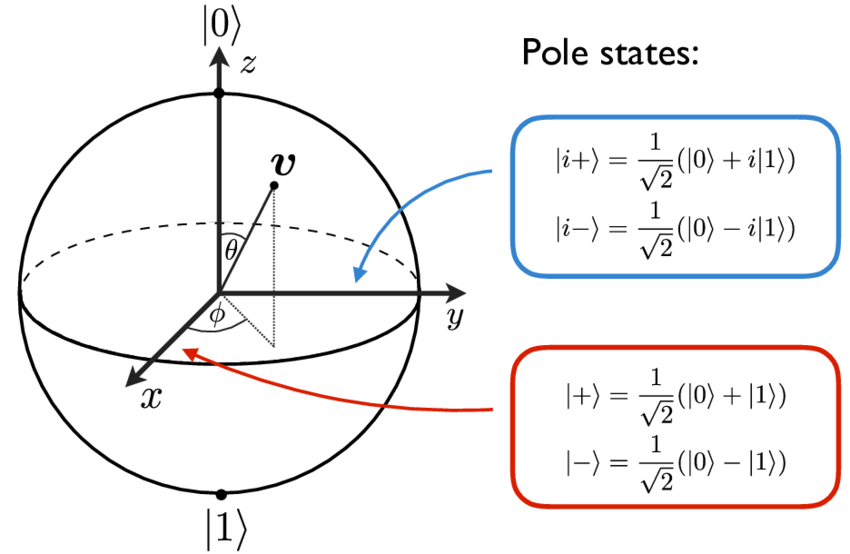
Superposition refers to the ability for a particular measurement, like position or velocity, to have multiple different possible outcomes each with an associated probability. The typical measurement used to define the zero and one binary states is called “spin”, which is best described as a kind of intrinsic angular moment for small particles. To visualize, you can think of the particle as having these two mutually exclusive states which lie on something called a Bloch sphere, visualized above, which represents the individual qubit with the north pole corresponding to the up, or 0, state and the south one corresponding to the down, or 1, state.

Entanglement is best described by example: particle A and particle B can have the property that, whatever state occurs for A, the opposite state occurs for B instantaneously. This means that particle A and particle B cannot be considered separately and must be treated as a singular object mathematically. Entanglement essentially allows quantum computers to combine the power of separate qubits. Interference refers to the ability for a property of one object to cancel or reinforce another. Interference occurs through something called “relative” phase differences, much like how the same waves can either interfere constructively or destructively depending on when they interact.

Although the analog has its issues, you can consider a superposition of entangled qubits as the quantum computer being able to occupy all input states at once and thus “compute” with all possible bit strings, a phenomenon called quantum parallelism. There is an issue when measuring the associated qubits: one likely gets the wrong answer. The trick is to find a clever way of destructively interfering with the incorrect solutions and constructively interfering with the correct solution, increasing the probability of measuring the desired result.

Although several quantum algorithms have been developed like Shor’s Algorithm for factoring large numbers efficiently, not many are as easily and beautifully conveyed as Grover’s Algorithm. Grover’s algorithm solves the problem of unstructured search, given a constraint for a solution: find the solution. It does the task with an advantage over classical computers, taking the square root of the time it takes a classical computer.

Initially, you put the quantum computer in a superposition of all possible input states through the use of the Hadamard gate. Mathematically, the Hadamard gate acts like a “quantum” version of the discrete Fourier transform which transforms phases with states and vise-versa, when operating on one bit. With the context, it makes sense then that the superposition is created by the application of the gate; it converts |0>, a vector of maximum state, into |+>, a vector of maximum phase, forcing each qubit’s state vector onto the equator of its Bloch sphere which puts it equidistant from the |0> and |1> states. The following is the state of an n-qubit quantum computer:

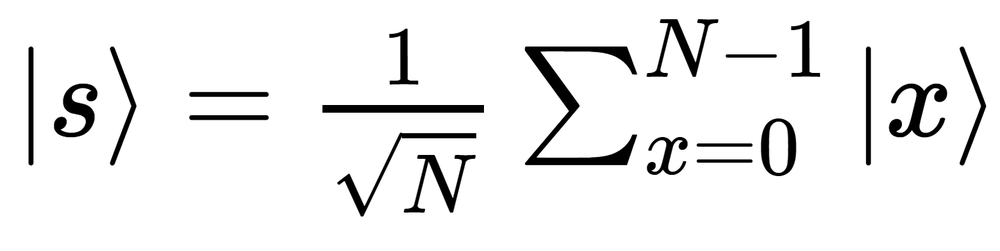
Mathematically, the left hand side corresponds to the state vector with a size equal to each possible input bitstring. The reason for the square root of N is to equally weight each outcome with the chance it occurs when considering measurement, which squares the state. If one were to perform measurements after this point, one would on average go through half of the possible bitstrings, making the algorithm take on order 2^n attempts before reaching the desired value, rather unimpressive.

Pretend, for the problem, you have a box called an oracle, which tells us if our answer is correct. If you want to interfere with the incorrect possibilities, you need to turn the oracle into an object which can introduce phase differences. The following represents such a circuit for the statement (a & b & c & d):

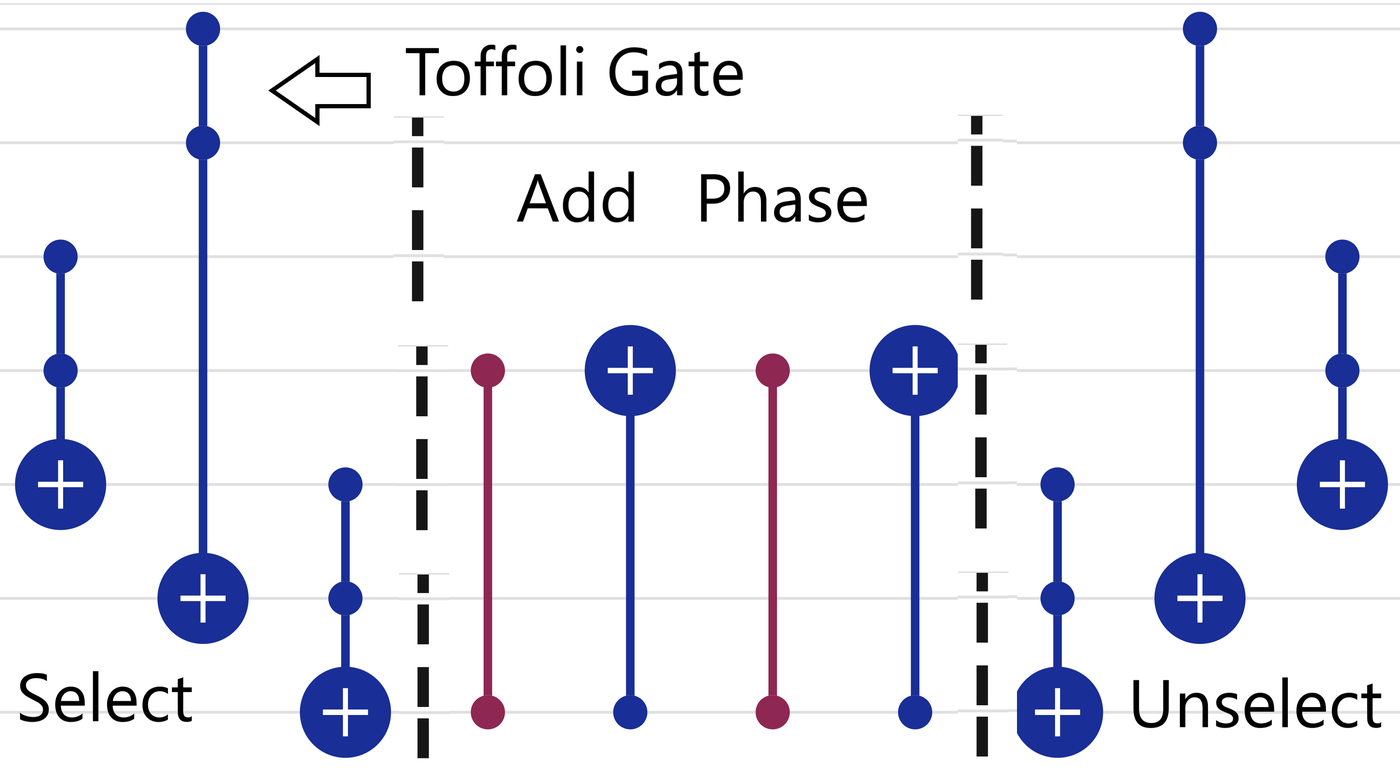
The gate with the two dots and plus sign is called the Toffoli Gate and it acts as a controlled-controlled NOT gate which flips the bit with a plus sign if and only if the two dots are true. The middle bit is called a CZCZ gate that introduces a phase to only the correct solution as it is only triggered if the oracle returns true. Now, our quantum circuit essentially initializes all possibilities and has a way of signifying the correct answer. The question is now how to make the correct answer available for measurement.

When plotting all states as a bar with negative phase flipping the bar over the x-axis, you can see the average has been shifted downwards, due to the phase flipping. So, instead of relying on the unmeasurable phase, you can choose to reinforce the probability of solutions that have a greater difference from the average phase. The greater the difference from the average, the higher the increase the probability of that solution which would mostly just consist of any desirable solutions.

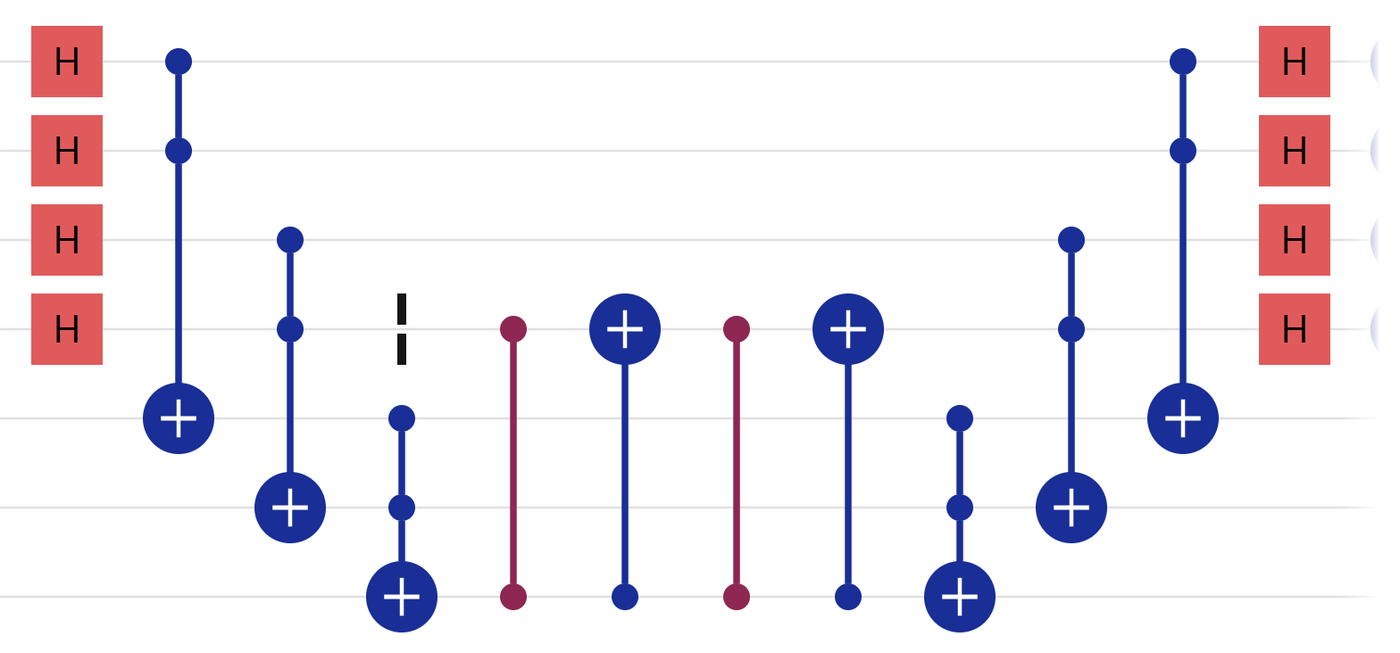
To cause such a rotation about the mean, one physically needs to interchange phase and state information, such that negative phase destructs while positive phase constructs—a process called amplitude amplification. Generally, such an operator is called a Grover operator. An implementation of the operator is shown above. You can think of the Grover operator as first converting phase to state information through the Hadamard gates, considering the phase of each possible bitstring, adding an amount of phase to the state in proportion to how much it differs from the rest, and, finally, interchanging the modified phase back to state information to influence the measurement probability.

The linearity of quantum mechanics allows a quite beautiful view of the algorithm described above through linear algebra. Using this, one can see that multiple applications of the oracle and Grover diffuser increases the probability of measuring the correct answer which increases with sin^2((r + ½)theta) where r is the number of Grover iterators. To, then, measure our desired state with reasonable probability, near one, one requires about sqrt(2^n) iterations.

As you can probably surmise, quantum computers are difficult to analyze and reason about algorithmically. Luckily, mathematics allows one to simplify away all the weirdness and to instead consider the nature of a quantum computer abstractly. Quantum computers are, in my view, exciting through allowing a whole new class of algorithms to exist with proven advantage in some cases. If you want to learn more, I suggest reading Qiskit’s Textbook and taking the Quantum Computing and Information Theory class, if it is offered in the future. If you want to explore the code used in this article, click on this link.